Table of Contents
Coordinate Transforms
Coordinate transforms lie at the heart of how MLR displays data on different base anatomies and how it keeps track of the location of ROIs. MLR coordinate transforms are based on the transformation information that is part of the Nifti image standard. You may want to also read the mrAlign manual.
Nifti Qform and Sform
Nifti specifies two coordinate transformations in the header of every image file:
- Qform is the coordinate transformation that takes the coordinates of the image into the coordinates of the magnet. It should be set in the data by the MRI image acquisition software.
- Sform in the context of MLR is a coordinate transformation that aligns the images to a standard reference, in our case the volume anatomy for the subject. It is usually set by mrAlign.
Both of these transformations have an associated code, qform_code or sform_code, that in MLR can be any one of:
- 0 the transformation has never been set
- 1 a transformation into magnet coordinates
- 3 a transformation into Talairach coordinates
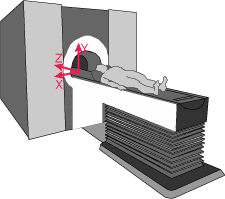
So, when your images come off of the magnet, they should start out with having their Qform set. This transformation then tells how to go from the coordinates of the image into the coordinates of the magnet.
What does this mean?
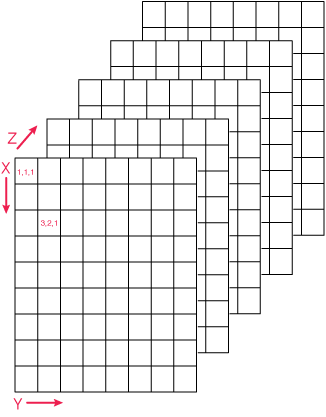
Well, if you have an image, then each voxel is labeled according to the [Ximg Yimg Zimg] location of where it is in the matrix specifying the image:
The Qform gives us a transformation matrix (though internally stored as a quaternion), that can convert the [Ximg Yimg Zimg] coordinate of the voxel in the image to the location in mm from the center of the bore [Xmag Ymag Zmag] where the center of that voxel lies.
Note how the magnet coordinates are in neurological coordinates. That is, the x dimension is such that the right of the brain is in the right of the image. Actually, it is more descriptive to say that the magnet coordinates use the LPI convention, because the first (x) dimension goes from Left to right, the second (y) dimension goes from Posterior to anterior and the third (z) dimension goes from Inferior to superior.
The transformation from image coordinates to magnet coordinats is done by multiplying the 4×4 affine transformation matrix specified by the Qform times the image coordinates [Ximg Yimg Zimg]: $$ \left\lgroup\matrix{x_{mag}\cr y_{mag}\cr z_{mag}\cr1\cr}\right\rgroup = \left\lgroup\matrix{rs_{11}& rs_{12} &rs_{13} &t_{x_{mm}}\cr rs_{21}& rs_{22} &rs_{23} &t_{y_{mm}}\cr rs_{31}& rs_{32} &rs_{33} &t_{z_{mm}}\cr 0 & 0 &0 &1\cr}\right\rgroup. \left\lgroup\matrix{x_{img}\cr y_{img}\cr z_{img}\cr1\cr}\right\rgroup $$
The Qform above is composed of a 3×3 portion that rotates and scales (specified by the rs's) and a 3×1 portion that translates (specified by the t's). Note that the coordinates have been made into homogeneous coordinates. This means that they have an added 1. This is a trick, the purpose of which is to allow us to do the translation and rotation in a single matrix multiplication.
The above Qform is really the combination of three transformations. A translation which specifies the distance in number of voxels to the center of the voxel at location [1 1 1]. A scaling which specifies the distance in mm between centers of voxels (this is usually the same as your voxel dimensions, unless, for instance, you put a gap between slices). And a rotation around the center of the bore of the magnet.
$$ \left\lgroup\matrix{rs_{11}& rs_{12} &rs_{13} &t_{x_{mm}}\cr rs_{21}& rs_{22} &rs_{23} &t_{y_{mm}}\cr rs_{31}& rs_{32} &rs_{33} &t_{z_{mm}}\cr 0 & 0 &0 &1\cr}\right\rgroup = \left\lgroup\matrix{r_{11} &r_{12} &r_{13} &0\cr r_{21} &r_{22} &r_{23} &0\cr r_{31} &r_{32} &r_{33} &0\cr 0 & 0 &0 &1\cr}\right\rgroup. \left\lgroup\matrix{s_{x} &0 &0 &0\cr 0 &s_{y} &0 &0\cr 0 &0 &s_{z} &0\cr 0 & 0 &0 &1\cr}\right\rgroup. \left\lgroup\matrix{1 &0 &0 &t_{x_{img}}\cr 0 &1 &0 &t_{y_{img}}\cr 0 &0 &1 &t_{z_{img}}\cr 0 & 0 &0 &1\cr}\right\rgroup $$
The units of the tximg are in voxels, the s's are in mm and the tmm are in mm in the rotated reference frame.
There is one little hitch with this. The Qform specifies the transformation where the image coordinates specify the origin as (0,0,0) rather than (1,1,1) which is what Matlab uses. So, actually to get into the coordinates of the magnet from the coordinates in the image, you need to shift the origin by -1 first:
$$ \left\lgroup\matrix{x_{mag}\cr y_{mag}\cr z_{mag}\cr1\cr}\right\rgroup = \left\lgroup\matrix{rs_{11}& rs_{12} &rs_{13} &t_{x_{mm}}\cr rs_{21}& rs_{22} &rs_{23} &t_{y_{mm}}\cr rs_{31}& rs_{32} &rs_{33} &t_{z_{mm}}\cr 0 & 0 &0 &1\cr}\right\rgroup. \left\lgroup\matrix{1& 0 &0 &-1\cr 0& 1 &0 &-1\cr 0& 0 &1 &-1\cr 0& 0 &0 &1\cr}\right\rgroup. \left\lgroup\matrix{x_{img}\cr y_{img}\cr z_{img}\cr1\cr}\right\rgroup $$
But, this is a detail. So we'll ignore it below.
Aligning across sessions
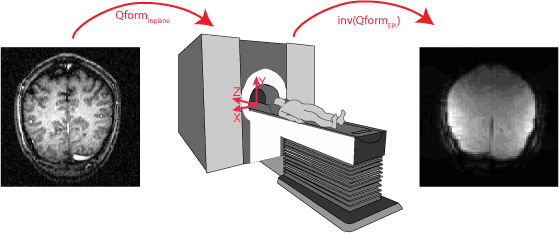
So, now we know how to transform the coordinates of an image into the magnet coordinates; we can now transform from one images coordinates into another images coordinates as long as they are collected on the same day. For example, if we want to find the location of a voxel in our inplane anatomy in the EPI image collected from the same day, we can transform through the magnet coordinates:
The Qform of the inplane (Qforminplane) transforms into the magnet coordinates and the inverse of the QformEPI takes you from the magnet coordinates to the EPI image coordinates:
$$ \left\lgroup\matrix{x_{EPI}\cr y_{EPI}\cr z_{EPI}\cr1\cr}\right\rgroup = \left\lgroup\matrix{Qform_{EPI}\cr}\right\rgroup^{-1}. \left\lgroup\matrix{Qform_{inplane}\cr}\right\rgroup. \left\lgroup\matrix{x_{inplane}\cr y_{inplane}\cr z_{inplane}\cr1\cr}\right\rgroup $$
Note that this does not assume that the inplane and EPI are taken with the same slice prescriptions. Since it uses the Qforms set by the magnet software, it will transform from inplane coordinates to EPI coordinates regardless of how the slices were placed in the inplane and EPI images. That is, as long as the subject didn't move their head in between the scans.
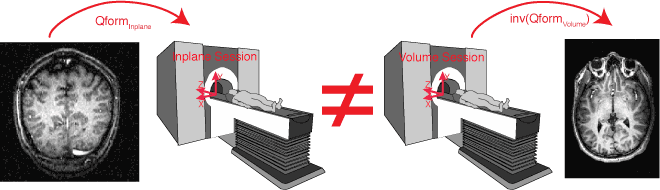
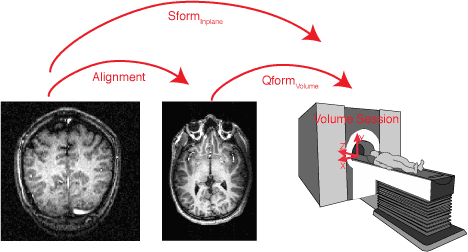
Now, what happens when we want to find where an inplane voxel comes from in the volume anatomy that was taken during a different session where the subject was not placed in exactly the same location in the magnet. In this case we have:
In this case, while the Qforminplane and the Qformvolume take the inplane and volume coordinates into the magnet coordinates, there is a problem: the subject's head was not in the same location on the two days that the inplane and volume images were taken. Thus, we can't compute the transformation from the inplane to the volume coordinates. We need an alignment:
mrAlign computes the alignment between the inplane images and the volume images based on trying to find the best match between the two images. A good starting place for this, is to initialize the alignment from the headers, which means to use the Qform information. As noted above this won't give a perfect alignment because the subject's head was in a different location on the two days. But, it's a good starting place and mrAlign will find a good alignment from there. Now, we know the alignment from the inplane to the volume and from the volume to the magnet on the day the volume was taken (Qformvolume). So, we can compute the transformation from the inplane to the magnet coordinates as if the head were in the same place on the day we acquired the inplane as the day we acquired the volume. mrAlign puts that transform into the Sforminplane.
$$ \left\lgroup\matrix{Sform_{inplane}\cr}\right\rgroup = \left\lgroup\matrix{Qform_{volume}\cr}\right\rgroup. \left\lgroup\matrix{Alignment\cr}\right\rgroup $$
So, the Sform contains the transformation of an image into the magnet space as if the head were in the same place as the day that the volume anatomy was taken. The Sformvolume is simply set to the Qformvolume since it already specifies the transformation of the volume coordinates to the magnet coordinates on the day that the volume was taken. (This is what mrAlign does when you set “Set Base Coordinate Frame” in the File menu).
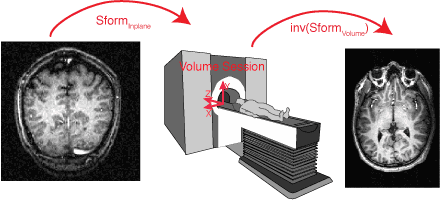
So, now that we have the Sforms set, the transformation from the inplane to the volume is easy. It looks like this:
So as long as the Sform is set in the same way, we can now compute the transformation from the inplane image coordinates to the volume coordinates. That is, to find which voxel in the volume ([Xvolume Yvolume Zvolume]) the voxel from the inplane image [Xinplane Yinplane Zinplane] comes from, the following computation is done:
$$ \left\lgroup\matrix{x_{volume}\cr y_{volume}\cr z_{volume}\cr1\cr}\right\rgroup = \left\lgroup\matrix{Sform_{volume}\cr}\right\rgroup^{-1}. \left\lgroup\matrix{Sform_{inplane}\cr}\right\rgroup. \left\lgroup\matrix{x_{inplane}\cr y_{inplane}\cr z_{inplane}\cr1\cr}\right\rgroup $$
You should never actually have to work with the Qforms and Sforms directly, though. If you ever need to explicitly do transformations, you should get the transformation matrices using viewGet. MLR will compute the correct transformations as discussed above using the Sforms. It will also take care of the shift by 1 (to account for Matlab's 1 based numbering system and the Qform/Sform's 0 based numbering system). There are transformations base2scan and scan2scan among many others. If you need the scan2base instead of the base2scan, simply use inv(base2scan). So to transform a coordinate in your base [X Y Z] to find its coordinate in the scan, you would do:
base2scan = viewGet(v,'base2scan'); scanCoord = base2scan * [X Y Z 1]';
You may want to round the scanCoords to the nearest voxel. Note that if you want to transform a lot of coordinates at the same time, X Y and Z should be row vectors (where the length is the number of coordinates). For example, to convert the points (1,5,1), (12,10,3) and (24,30,5):
X = [1 12 24]; Y = [5 10 30]; Z = [1 3 5]; baseCoords = [X;Y;Z;ones(1,length(X))]; base2scan = viewGet(v,'base2scan'); scanCoords = base2scan * baseCoords;
All coordinate transformations in MLR are handled in a similar way, be they from a base anatomy coordinate to a scan (epi) coordinate, or even from one scan coordinate collected on one day to a scan coordinate collected on a different day. ROIs inherit the Sform (and the voxel size) of the base anatomy that they were defined on, and then from there the transformations work in an analogous way. If you want to get ROI coordinates in the scan or in a base anatomy, you should always use MLR functions loadROITSeries or getROICoordinates which use the function xformROIcoords to transform the ROI coordinates. This is because xformROIcoords does some extra processing to try to maintain ROI volume across different voxel sizes.
-jg.